...Instructive...
|
< THE HELICOPTER BLADE > |
|
You want to understand how an helicopter blade works? You'd better read that first and then go to scientific documents for more details. |
< in the body of the text, the symbol « Ò » refers to the mathematical model of the rotor hovering>
| HHH |
| HHH |
| Reminder about airfoils |
|
Geometric parameters of an airfoil are defined in general by :
Example of « S » airfoil : mean line is convex at leading side and concave at trailing side: |
Vertol
V2310_1.58 (« S » airfoil)
| Airfoil behavior |
|
The airfoil behavior depends on the different modes of operation of the enclosing boundary layer when it moves at a defined velocity through the air. The boundary layer is characterized by an intense shearing of air particles from the airfoil surface (at the airfoil surface particles are stuck by viscosity : velocity to airfoil is null, max velocity regarding the incoming airflow) up to where the particles reaches the velocity of the incoming airflow (max velocity to the airfoil, null velocity regarding the incoming airflow). The followings can be considered :
|
|
 |
|
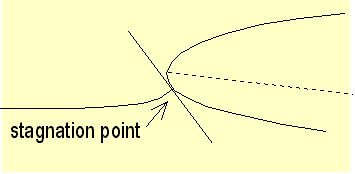
The graphic below shows the velocity distribution of an Eppler 201 airfoil at an angle of attack of 6 degree |
It is usual to call velocity from infinity (V) by designating the velocity and the direction of airflow to the airfoil, in practice at a point distant of several chords from the airfoil. Bypassing the airfoil, the flow is subject to acceleration/deceleration and its related velocity (v) varies considerably. At the stagnation point the related velocity (v) is null. Then following the ratio (v/V) on the upper surface, values in the order of 2 can be reached in the first percent of the chord (considerable acceleration generated by change of direction and strong suction) then it decreases steadily toward 1 close to the trailing edge. On the lower surface the flow acceleration is smooth and stabilizes its ratio (v/V) below 1 (velocity lower than the velocity from infinity). The surface enclosed between upper and lower velocity is proportional to the lift. In case the lift is null, the two curves overlap in such a way the enclosed surfaces come to neutral. |
|
Air velocity variations within the thickness of the boundary layer are not the same in laminar region and turbulent region : it is steeper in the turbulent region (velocity gradient higher producing more friction). As long as the boundary layer is laminar or turbulent the lift coefficient (Cl) is not affected. It is only the case if there is separation of the boundary layer from the airfoil, resulting in the stalling effect. The target consist in keeping the boundary layer in laminar rate as far as possible on the upper side to take advantage of low friction. When increasing the attack angle, stalling conditions are created : the separation point at the trailing edge appears traveling on the upper surface towards the leading edge, while the stagnation point moves lightly backwards on the lower surface (up to a tens of % of the chord). To fulfill the laminar rate conditions, it is required that the airfoil shaping manages at best possible the kinetic energy provided by the upper airflow to make it easy to reach the trailing edge (at this point the flow velocity is about 85% of the velocity from the infinite). If flow lines take off the airfoil surface there is separation of the boundary layer and drastic increase of the drag. For some airfoil, depending on their upper curvature, separation might take place and followed by a reattachment of the boundary layer : a bubble is so created enclosing a turbulent mode (drag +++) and sometimes announcing the stall. Some techniques have been implemented to re establish the laminar rate by sucking the bubbles. Similarly bubbles at the upper leading edge can occur, if the curvature radius is low, under the strong acceleration of air particles combined with the centrifugal force. |

|
The surface finish has an important impact on the boundary layer and the related friction. A fine carborandum surface type can turn a laminar rate into a turbulent one. This mean (so called turbulator) can be placed at the leading edge to delay the stall thanks to the stability of the turbulent boundary layer, the drag being unfortunately increased at low angle of attacks. Airfoils
are characterized by three basic coefficients : drag, lift and moment,
measured in wind tunnel mainly as a function of angle of attack and Reynolds
number. Knowledge of these coefficients is required to compute aerodynamic
forces. The relative thickness, the leading edge curvature radius and the
camber impact airfoil coefficients :
An airfoil is designed and selected for a given application (environmental conditions, Reynolds number, Mach, angling range, etc...). In general for a helicopter, the followings are looked for :
|
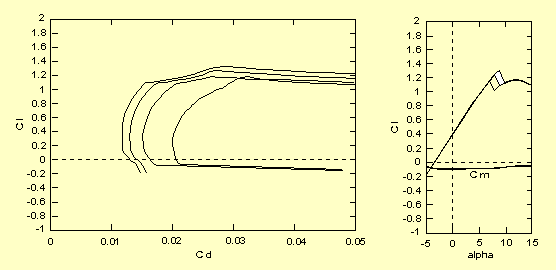
Cl, Cd, Cm curves for Reynolds number : 160000, 120000, 80000, 40000
(alfa : attack angle)
| General conclusions about airfoil efficiency |
|
| Reynolds and Mach numbers |
|
The Reynolds number is a figure without dimension that characterized the flow rate of a fluid around a body (i.e. a wing airfoil). It is defined by the following equation : Re = L.V / n where :
This number, related to the ratio between inertia and viscosity forces, has a major impact in the subsonic domain where these two types of forces are dominating. At low Reynolds number (low speed) viscosity forces are dominant resulting in « laminar » flows. At high speed, the importance of inertia forces make the flows « turbulent ». In case of two homothetic airfoils with different chords (for instance comparing scale and full size models), operated at the same angle of attack, produce airflow practically similar at the same Reynolds number (velocity and pressure distribution, forces are determined by similitude). In those conditions drag coefficients are the same. The knowledge of drag as a function of Reynolds number helps to define the behavior of an airfoil whatever its dimension and speed are. As an example, in the case of a blade the Reynolds number depend on the speed at the related radius ; the drag coefficient can then be calculated for every sections thanks to a corrective formula (hyperbolic function).
Under the effect of speed, the air is compressible leading to airflow modifications. The three Cl, Cd, Cm coefficients are affected and can be corrected according to a simple formula depending on the Mach number. The effect is most sensitive in the velocity range between 0.3 Mach and 0.8 Mach. |
| Aerodynamic of the blade |
|
A helicopter rotor includes several blades (multibladed rotor) which have similar geometry regarding those of airplane wings. However, three main phenomena particular to rotary wings have to be considered :
To get
a correct analysis of the blade in action, it is necessary to divide the
radius in a large number of stations, each one having its own conditions
of operation : speed, angle of attack, CL, Cd, Cm, etc...) The aerodynamic
study is made considering, at least in a first time, that the airflow is
inscribed in the airfoil plane (two dimensions airflow). The chord and
the direction of null lift is defined as in the case of a wing. The plane
perpendicular to the rotor axis is designated as driving
plane and gets an essential status.
Wind combinations
|
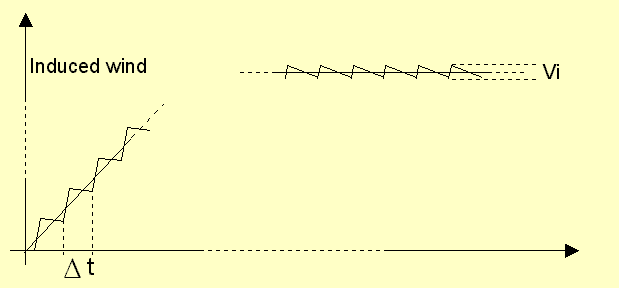
|
|
The total effective downwash seen by the blade is then the sum of the Froude wind (VF) plus the half peak value of the blade induced wind (1/2Vi).
|
-
helicopter and wind speed (Vo)
|
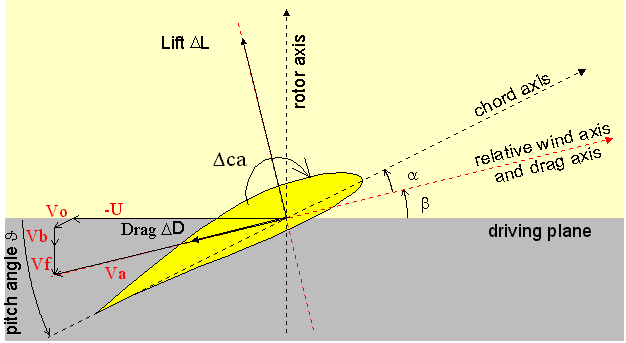
H
H
H
Drag and lift forces result from the airflow circulation through the rotor in accordance with the previous definitions. The drag is carried by the relative wind axis and the lift is perpendicular to it. |
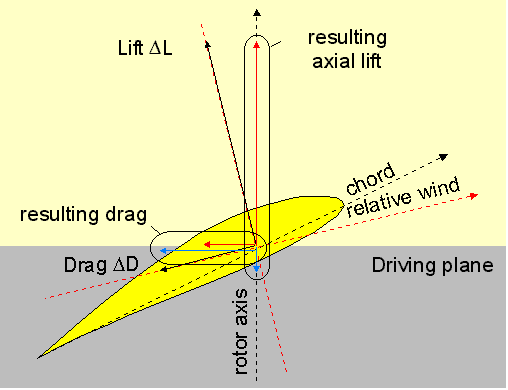
|
As drag axis and lift axis are inclined of the relative wind angle, it is necessary to project both lift and drag onto the rotor axis on the one hand and on the driving plane on the other hand to get the resulting axial lift and the resulting drag. The resulting axial lift «Ò» is the combination of the lift projections plus the drag projection on the rotor axis (this reduces the lift). The resulting drag is the combination of the drag projections plus the lift projection on the driving plane (this increases the drag). The resulting drag is at the root of the axial torque«Ò» and of the required power under the form of specific power «Ò» expressed in W/kg (specific to the lifted mass unit). One should notice that the axial lift is in deficit regarding the lift itself and the resulting drag is in excess regarding the drag itself. This corresponds to inevitable losses : less lift and more drag are obtained. Also, it can be seen that the greater the angle of attack and the relative wind angle are, the more losses appear ; this being more significant when the lift is important compared to the drag. In fact it is of current use to consider the resulting drag as the sum of a so called shape drag (specific to airfoils and viscosity constraints) and an induced drag (resulting from the lift projection). To generate a given lift, at a given chord and rotor diameter, a cambered airfoil gets this results at low angles, causing a lift less inclined and less induced drag. This is an important factor that allows to minimize the losses but only a complete computation «Ò» helps to find the optimal solution. Don’t forget however that the more « power consuming » parameter is the rotation speed that impacts the power by its square value. |
| Combined constraints |
|
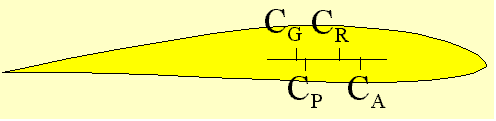
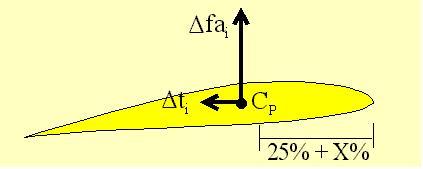
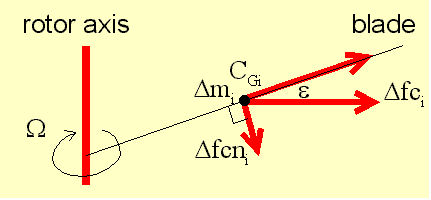
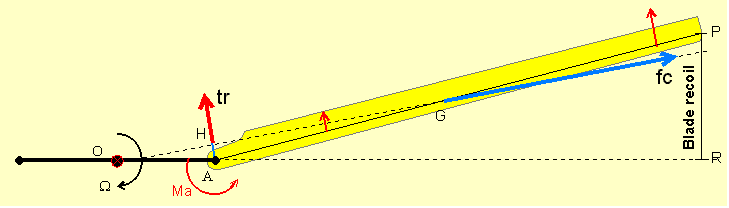
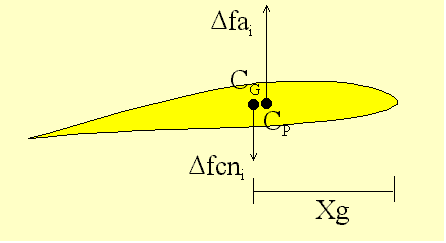
Center definitions The gravity center (CG) is the internal point of a blade that enables to keep the blade balanced whatever its orientation is. It is at this point that gravity and centrifugal forces applies. Knowing this point enables to calculate the blade moment (static moment) which is the product of the distance of the gravity center to the rotor axis by the blade mass. The gravity center (or at least its projection on the upper surface) can be easily determined : for that, protect the foreseen area with a sticker and balance the blade (lower side up) on a cutter edge via two oblique orientations. The junction of the two marks provides a very good estimate of the X, Y location. Don't forget that when analyzing a blade station per station, each station has a mass and a center of gravity by itself, located in general at the same distance from the leading edge than the resulting center of the complete blade only in case of rectangular top view. The natural location of the center of gravity for a blade made with homogenous material is in the 40% region from the leading edge (at least for current cambered airfoils). The aerodynamic center (CA) of any airfoil is the point located by convention at 25% of the chord from the leading edge. At this point the moment coefficient is practically independent from the angle of attack (or at least this is the point where it is the less dependent). This coefficient value is either null for a symmetrical airfoil or negative for a cambered airfoil. Airfoil data give the coefficient value implicitly linked to the aerodynamic center. The lift center (CP) «Ò» of any airfoil is the point where the resulting moment is null and consequently the resulting aerodynamic force only applies at this point. In case of symmetric airfoils the aerodynamic center and the lift center are merged. In case of cambered airfoils, the lift center is generally back to the aerodynamic center and all the more as the camber is important (from 25% for symmetrical airfoils it can move back to 50% for some cambered airfoils). The lift center can be derived from the aerodynamic center applying a conversion to the system of forces (see the related window hereafter). In case of cambered airfoils, the lift center travels forward when increasing the pitch angle so progressively coming closer to the aerodynamic center.
The rotation center (CA) is the mechanical point round which the blade rotate (feathering). The longitudinal or span wise axis goes through this point. Its position has no influence on the blade twist and is of little effect on the resulting moment of the blade and also about the control constraints. For any airfoil and to minimize the twist effect (further explained), it is ideal that the average location (span wise) of lift center merge with the gravity center. This common location is then at 25% for symmetric airfoil (lead insertion at the leading edge to get the balance) and can be in the order of 40% for cambered airfoils (no lead required). |